■　問題

サイコロを振って、初めて2の目が出るまでの試行回数は、平均で何回か[20]。

■　シミュレーション方法

「確率とは何か」を使って、サイコロを振って、2の目が初めて出たときの試行回数をノートに記録してみよう。「初めて2が出る」までの試行を20回繰り返した結果を、縦軸に頻度(度数）、横軸に「初めて2が出る」までの試行回数をとってグラフにした。このようなグラフを「ヒストグラム(histogram)」という。横軸であるが、2というのは「2以下の試行回数」で、4は「4以下で、2よりも多い」試行回数、・・・という意味で、これらは「階級(class)」と呼ばれる。

「階級」をどのように定めるかについての、定説はないが、「階級」の決め方によって、ヒストグラムの「見栄え」は異なる。一般には、5から15くらいの階級数がよいであろう。目安として、階級数(K)は、データ数をNとするなら、

とする考えもある[19]。logは2を底とする対数である。

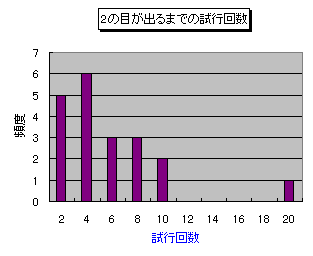
この実験での平均値は5.15である。しかし、20回のシミュレーションではなく、もっとシミュレーションを繰り返さなくては、初めて２の目がでるまでの平均試行回数はわからない。が、このヒストグラムから、頻度のもっとも多いのが4である。これは「2より多くて、4以下である」から、「3または4」ということになる。つまり、サイコロを投げると「3または4」回目に初めて2の目が出たことがもっとも多く観測されたことになる。3と4の中間値は3.5なので、これをこの階級の「階級値」という。

階級値が3.5のとき、もっとも頻度が多い。このような最頻値をモード(mode)という。

もっと見やすくするために、階級値を横軸にとって、グラフを書いてみた。

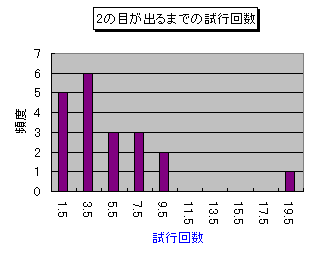
しかし、問題の質問は、サイコロを振ると「平均で何回」目に2が出るか、である。モードではない。

ということは、やはり解答は平均値に近い値でなければならないだろう。シミュレーションの回数をもっと多くすれば、解答を推定することは可能だが、解答は期待値の定義から簡単に得ることができる。

■　解答

2が出るまでの平均試行回数をmとし、以下2つのケースに着眼する。

1. サイコロを振って1回目に2が出なかったら、2の目は2回目の試行以降に出ることになる。この場合、2が出るまでの平均試行回数は
   1 + m

   である。(1回投げているので、1をmに足す。)

2. サイコロを振って、運良く1回目に2の目が出る場合も考えられる。この場合の確率は1/6で、平均値は1である。(1回しか投げていないので。)

したがって、1回目に2が出ない確率は5/6である。

以上の2つのケースから、2が初めて出るまでの平均試行回数は

と計算できる。この式をmについて解くと、m=6である。

解答は「6回」ということになる。

これは、シミュレーションの平均値に近いが、シミュレーションの回数を20回よりも多くすれば、もっとこの解答に近い平均値が得られたはずである。