![]()
■ 問題の提起
少ない数の事例から規則性を発見することは難しい。が、事例の数が多くなると、何らかの規則性について推論することが可能となる。
例えば、「硬貨を投げる」という簡単な実験を考える。硬貨の表が出た回数を数えて、投げた回数(試行回数)で割ると、「相対度数」が得られる。
硬貨に何ら細工が施されていなければ、表と裏の出る確率は「同様に確からしい」。が、仮に何らかの細工があって、表の方が出る確率が高ければ、表と裏の出る確率は「同様に確からしい」とはいえない。
硬貨を精密機器などを使って調べる方法もあると思われるが、硬貨を実際に投げて調べる方法もある。これは、実験によって調べる方法であるが、この実験によって解答が得られる根拠は、試行回数が多くなると、硬貨の表が出るという事象に何らかの規則性を見いだすことができることである。
ようするに、事象の確率とは、数多くの試行結果において事象が起こるであろう回数の割合である。このような割合(相対度数)についての妥当な推定値を期待値という。
なお、「試行」や「相対度数」などの確率論用語については、確率とは何かを使って学ぶことを推奨します。
■ コンピュータ・シミュレーションによる実験
実際に硬貨を何回も繰り返し投げるのは無理である。硬貨投げ実験の装置を作ることも考えられるが、コストがかかる。
そこで、コンピュータを使って硬貨投げの実験を行ってみよう。確率とは何かを使い、硬貨を10回、20回、500回、・・・と10万回まで投げてみた。相対度数をグラフにすると、以下のような結果が得られた。
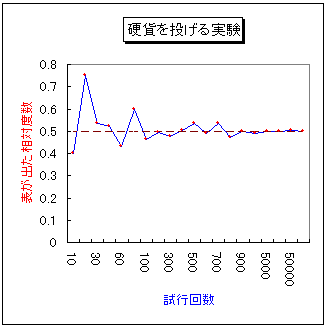
試行回数が増えるにしたがって相対度数が0.5に収れんしていくことがわかる。ここで、「収れん」とは、0.5からの「振れ幅」が小さくなっていくことを意味する。
このグラフを見ると、試行回数がかなり多くならないと、公平な硬貨を投げて表が出る割合(=確率)は「0.5であろう」という推論結果が得られないことがわかる。
硬貨に何らかの細工があるかないかを調べるには、硬貨を自動的に投げる装置などをつくって何万回と投げてみなければ結論を得るのは困難である。また、細工によって表が出る確率が0.51と50%から1%の違いしかないなら、試行回数を何回以上にすれば、1%の違いを発見することができるのか?
確率とは何かの「降水確率」のシミュレーションでは、確率を設定することができるので、この問題に挑戦してみてください。
■ 期待値とは
硬貨投げの実験をゲームと考え、表が出たら100円の賞金が出て、裏のときは賞金はゼロとしよう。硬貨には何ら細工はなされておらず、表と裏が出る確率は「同様に確からしい」と仮定する。つまり、このゲームで使用される硬貨は「公平」なのである。
このようなゲームの期待値(「数学的期待値」ともいう)は、
である。
ところが、一回の試行で50円が利益として出ることはありえない。一回の硬貨投げでは、100円かゼロである。
しかし、このゲームを何回も繰り返して行うとき、投げた回数の約半分は100円の利益が出る。これは、上のグラフを見れば明かではないか。
つまり、期待値とは試行回数がじゅうぶんに多いときの平均利益についての妥当な推定値なのである。期待値は「平均値」とも呼称される。
■ オプション取引への応用
オプション・デルタはヘッジ比率という使い方の他、その絶対値を取って、「権利行使される確率」と考えることができる。
例えば、アット・ザ・マネー近辺のデルタはコールもプットも約0.5である。1/2の確率で権利行使されるということは、1/2の確率でイン・ザ・マネーになるということでもある。
しかし、1/2の確率とは、2回の取引のうち1回は勝つという意味ではない。「デルタが1/2のときの取引を何回も実行すると、約半分の取引では勝てるであろう」という意味である。
したがって、オプションを買う場合は、権利行使されることによる損失は発生しないので、デルタは1に近いほど勝率は高くなる。が、実際はデルタが大きくなるとイン・ザ・マネーになるため、プレミアムが高くなる。
ここに、問題がる。高いプレミアムでデルタが1に近いオプションを買っても、相場が動いてデルタが落ちてしまうこともある。デルタの相場に対する感応度はガンマで見るが、原資産(または原市場)価格を入力してデルタを再計算すると、わかりやすい。また、価格弾力性(オメガ)によって、プレミアムの上昇具合(レバレッジ効果)はさらに明確になる。
オプション取引での勝敗は、相場の動きに依存するが、相場の動きのみに依存するという見方は誤りである。相場があまり動かなくても、残存日数やボラティリティーがデルタに与える影響は大きい。また、相場が動いてもボラティリティーの変動によってデルタの動きが左右されることもありえる。
オプション取引は、先物などと違って、数多くのリスク要因によって影響を受ける。オプション取引はダイナミックな多次元ゲームなのである。
デルタなどリスク指標の計算は
などで、簡単にできる。
しかし、確率としてのデルタだけを見ていては、リスクは総合的に把握できない。ポジション・デルタを見るべきである。デルタをヘッジ比率とみると、オプションの買いと売りの混合によってデルタの総合計をゼロにすることが可能である。オプション用語で、「デルタ・ニュートラル」といい、このときのリスクはゼロになる。相場の変動に対しどこまでデルタ・ニュートラルを維持することができるかは、ポジション・デルタのシミュレーション結果を見ればよい。
ポジション・デルタのシミュレーションはTraderを使えば簡単にできる。
デルタは確率とポジションの両サイドから見るべき指標である。