■　期待値の定義

期待値については、すでに少し述べた。が、ここではもっと数学的な定義をする。期待値がわかると、確率分布も容易に理解できるからである。

離散型の確率変数Ｘ(大文字のＸ)が取りうる値を、Ｘの小文字に添数iを付けて、

と書く。Ｘが取りうる値は

と書くことができる。また、添数iを

と定めると、iによってランダム（でたらめ）な実験・試行の結果(事象）を数えることができる。

確率変数の値x_iに、それぞれの値が実現する確率p(x_i)をかけたものの和を期待値(数学的期待値）または平均値という。期待値は英語でexpected valueまたはexpectationなので、頭文字のEを使って「Ｘの期待値」という意味で、期待値をE[X]と書くと、

によって期待値を求めることができる。

少々、記号が多くなり、記号の意味が重要になったが、数学の発展とは記号の発展のようなところもある。概念や考え方などを記号によって簡潔に表現することで、論理的な展開が明確になるためであろう。

■　期待値の計算例

●　硬貨投げ

硬貨投げの場合、事象は2つしかないため、i=1,2である。したがって、X=x₁,x₂となり、確率変数には2つの値しかない。

とすると、硬貨投げの期待値は

と計算できる。

ただし、これは表を1、裏を0と決めた場合の値である。

硬貨を投げたときの事象を横軸、それぞれの事象が実現する確率を縦軸にとり、グラフにすると以下のようになる。このように事象が実現する確率を表わしたものを確率分布(probability distribution)という。

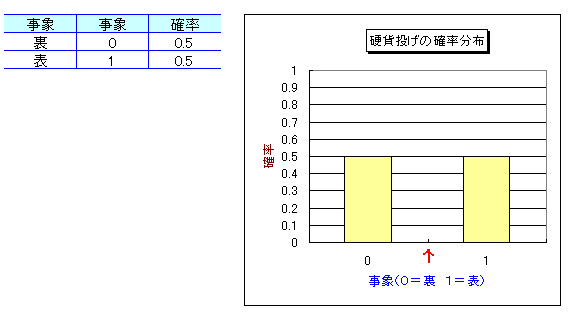
赤い矢印で示したところが期待値（0.5)である。硬貨を投げて表と裏の間の値である0.5が出ることはありえない。が、これはあくまでも数学的期待値である。この期待値が意味するのは、「硬貨を何回も繰り返し投げると、約半分は表が出ることが期待される」、ということである。　

●　サイコロ振り

サイコロを振って賞金が当たるというゲームの期待値を計算してみよう。

ルールは簡単で、サイコロを振り出た目によって以下のように受取金額が決まる。ただし、サイコロを振る前に300円の参加料金を払わねばならない。

サイコロには6つの目があり、それぞれの目が出る確率が等しいと仮定する。それぞれの目が出る確率は1/6となり、各受取金額がもらえる確率も1/6となる。Ｘをサイコロの目とすると、このようなゲームによってもらえる金額の期待値E[X]は

　　　　　　　　　　　　　　　　　=350円

である。

ゲームへの参加料金が300円なので、このゲーム期待収益率は

となる。

このゲームをすると、必ず16.7%の収益率（リターン）が出るという意味ではなく、「何回もこのゲームを繰り返すと、長期的な平均値として、収益率が16.7%に収れんすることが期待される」、という意味である。

このゲームの確率分布は、このようになる。

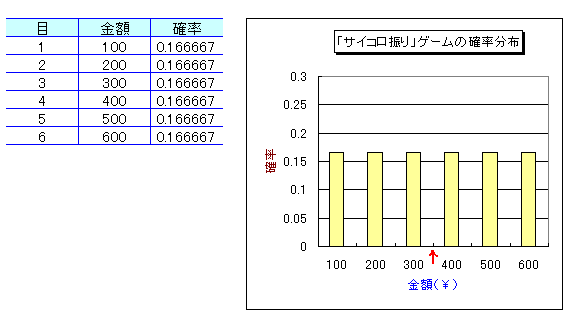
赤い矢印で示したところが期待値（350円)である。硬貨投げのゲームと同様、各試行においてこの期待値が出ることはありえない。が、「このゲームを何回も繰り返すと、平均的には、350円が手に入る」というわけである。そして、参加料金が300円なので、「長期的にみると16.7%のリターンが出る」ことが期待される。したがって、このゲームは、主催者よりも参加者にとって得なゲームである。もし、参加料金が350円なら、長期的なリターンは0%なので、主催者にとっても、参加者にとっても「公平」なゲームである。