■　定義

平均とはヒストグラムや度数分布を代表する値である。ヒストグラムなどは視覚的にデータを表現しているが、平均という数値を使うことで、データの特徴を簡潔に表現することができる。

データの代表値として、もっともよく知られているのが、平均(mean or average)である。平均には、

1. 算術平均(arithmetic mean)
2. 幾何平均(geometric mean)
3. 調和平均(harmonic mean)

などがある。

この中で、一般に「平均」として知られているのが、算術平均である。この平均値はデータを足した和をデータの数で割ったものである。

この講座では、算術平均のみを使用する。

■　「平均」の落とし穴

平均には「落とし穴」がある。平均とは、30とか187などと、ひとつの数字にすぎない。したがって、頭をオーブンに突っ込んで足を冷凍庫に入れ、「平均体温は37度です。正常です」などということになりかねない。

平均とはあくまでもデータの「重心」のようなものである。したがって、データの中にひとつでも大きな値(または小さな値）があると、このような「極端な値」の影響を平均値は受けやすい。必ずしも、平均値はデータの「真ん中」の値ではない。

例えば、

というデータの平均値は

である。2はデータの「真ん中」の値である。2を境にデータは

と

に分かれるからである。平均値2を境にデータの数は1つずつに分かれる。つまり、データは「左右対称」なのである。

ところが、3を6にすると、データは

となり、平均値は

となり、平均値は6の方へ近づく。3は「真ん中」ではない。つまり、3を境にデータは

と

に分かれる。データは左右対称ではなくなった。

■　メディアン

平均では、データが左右対称でない限り、どのような数値を境にデータが2つに分かれるかを知ることはできない。

そこで、用いられるのが「メディアン(median)」である。(中位数または中央値とも呼ばれる。)

メディアンは「極端な値」に引っ張られず、データの真ん中の値を示す。計算方法はデータを小さいもの(または大きいもの）から順番に並べて、ちょうど真ん中の値を取るだけである。データが奇数のときは、真ん中の値はすぐに決まる。が、偶数のときは、中央に位置する2つの値を足して2で割った値をメディアンとする。

例えば、奇数個のデータ

のメディアンは3である。

偶数個のデータ

のメディアンは

である。

データの半分はメディアンより小さく、残りの半分は大きい。

■　為替レートの平均とメディアン

以下は為替レートのヒストグラムである。

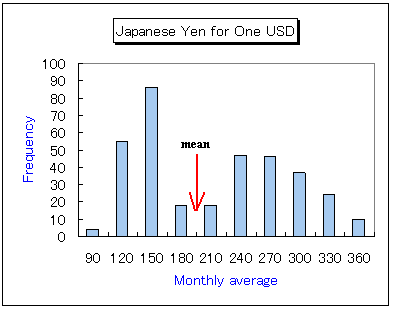
meanと赤い矢印で示したのが、この分布の平均(196.75円)である。この分布では、平均の左右に「山」がある。したがって、為替レートが平均近辺になることは、あまり起こりうることではない。

また、この分布のメディアンは200.51円である。このレートを境にデータは2つに分かれ、半分がこのレートより安く、半分がこのレートより高い。

ということは、ドル相場が100円から150円の間で推移する「円高時代」では、ドルがいきなり200円前後になることは、「過去のデータ」からはありえない。

平均もメディアンも、このような「円高時代」を「代表する値」とは言い難い。

つまり、為替レートは85年のプラザ合意を境に「2つの分布に分かれた」というべきであろう。このような見方は、平均やメディアンでは、できない。

したがって、相場を読むとき、平均などだけでは、誤った判断に陥る危険がある。相場はヒストグラムで見るなど、色々な方向から分析するべきである。

■　パーセンタイル(percentile)

メディアンの概念を拡張したのが、「パーセンタイル」である。分位点ともいわれる。

データを小さいものから順番に並べ、小さい方から100p%の位置にある値を「100pパーセンタイル」または「百分位点」という。pは0以上、1以下である。

よく使用されるパーセンタイルに、四分位点(quartile)がある。これは、小さいものから順番に並べられたデータを4等分したときの3つの分割点のことである。したがって、このようなパーセンタイルは

1. 25%分位点(Q₁と略す)
2. 50%分位点=メディアン
3. 75%分位点(Q₃と略す)

となる。

Q₁とは、データの25%がこの値よりも小さいことを意味する。Q₃とは、データの25%がこの値よりも大きいことを意味する。

では、為替レートのパーセンタイルを見てみよう。

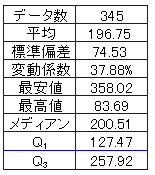
為替レートの1/4(25%)が127.47円より「円高」で、1/4(25%)が257.92円より「円安」になっていることがわかる。

このように、データを統計的にまとめて見ると、現在の為替レートがどのような水準にあり、どのようなレートが「妥当」な水準かが見えてくる。また、平均レートからQ₁とQ₃が約70円ほど離れていることから、このデータには大きな「ばらつき」があることもわかる。

1971年1月から1999年9月までの為替レート(月平均）のデータでは、1/4が127.47円より「円高」であるから、ドルが100円前後で推移することは、歴史的にみると稀なことである。が、ヒストグラムを見ると、大きく分けて、2つの分布(「山」)がある。この山の「谷間」は85年のプラザ合意に起因している。したがって、ドルが100円前後で推移する時代は、ニクソンショック以降の経済において、稀なことではあるが(起こる「確率」が小さいこと)、明らかに「円高時代」へのシフトを意味している。

■　累積相対度数

為替のヒストグラムで、下の階級から順に度数を積み上げたときの度数を「累積度数(cumulative frequency)という。そして、累積度数を相対度数で示したものを「累積相対度数(cumulative relative frequency)」という。為替レートの累積相対度数は以下のグラフのようになる。50%のところがメディアンである。

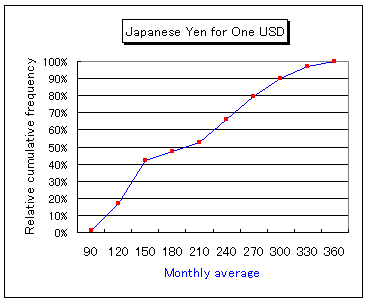
データをこのようにして見ると、300円以上の円安や110円以下の円高は、1971年1月からの推移によると、「起こりうる確率」としては、約10%以下ということが一目でわかる。これも、「1ドル100以下」時代が、これまでとは異なった時代であることを示唆している。

■　平均からの「ばらつき」について

「ばらつき」はリスクの指標である。価格変動が大きいほど、相場では損失も大きくなる。統計学では、「ばらつきの尺度」として「標準偏差」が使われる。

「変動係数(coefficient of variation)」とは、標準偏差値を平均値で割って百分率で表示したもので、変動係数が大きいほど、ばらつき(すわわちリスク）が大きい。

「標準偏差」については、次の講義で述べる。