■　データ

為替レートは米ドルのレートで、ニューヨーク電信決済での月平均レート。出典はアメリカ連邦準備局データ。

期間は1971年1月から1999年9月まで。

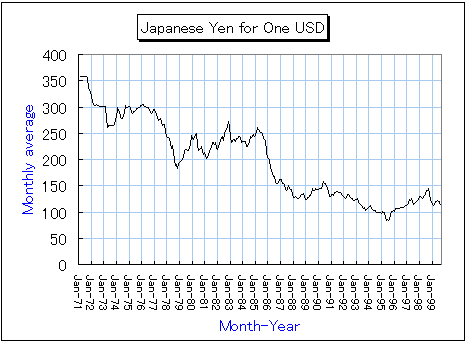
この期間におけるデータの基本統計は、以下のとおり。

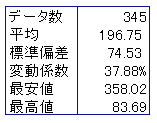
標準偏差(standard deviation)とは平均からの「ばらつき」を示し、データの約3分の2が

と

の間に入っていることを意味する。標準偏差値が大きいと、平均値からの「ばらつき」も大きい。ボラティリティーはこのような標準偏差値のことである。(正確なボラティリティーの計算方法はもう少し複雑であるが、基本的概念は「ボラティリティー＝標準偏差値」である。)

変動係数(coefficient of variation)とは、

で、この値が大きいと変動(「ばらつき」）も大きい。

階級数は、

なので、10とした。(log₂X=1.443lnXと換算できるので、通常の電卓で計算できるはず。)

■　ヒストグラム

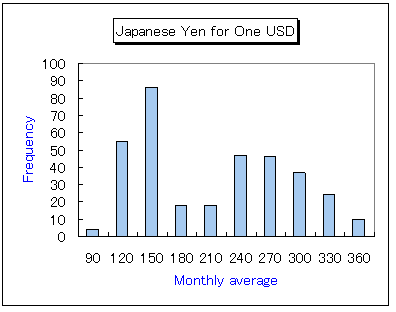
このヒストグラムを見ると、最頻値(ピーク）が2つある。ひとつは120円から150円で、もうひとつは240円から270円あたりである。

階級数が少なすぎると、このようなピークを見落とすことになろう。また、階級数が多すぎるとピークがわからなくなる。階級数をどのように設定するかは、大切な課題である。

このようにピークが2つある分布をbimodal distributionという。「モード」が2つあるという意味である。

■　予測における意義

ヒストグラムを見るとピークが2つある。ばらつきを見ると、240円から270円あたりでドルは大きく変動し、120円から150円あたりでも大きく動いた経緯がわかる。つまり、これらのピーク近辺での為替相場のボラティリティーが高かったことを意味している。

したがって、過去のデータを使って相場を予測するとき、ピークが複数ある場合、データは分けて使用しなければならない。単に過去の10年分のデータすべてを使って相関などを見ても、データ数が多くなると相関は高くなる傾向があるので、あたかも相関があるようにみえることがある。これは落とし穴である。

為替相場でのボラティリティー計算などでは、最近のデータにこそ意味があると思われる。71年から99年までの為替レートの平均値は約200円である。99年9月の時点で、このような相場水準にいきなり戻ることは、ありえない。また、ヒストグラムを見ると、200円は2つのピークの「谷間」でもある。ということは、200円でドルが取引される頻度(確率と考えてもよい）は比較的少ないという意味である。

このように、「平均値」というのは、データをヒストグラムによって視覚的に見ない限り、場合によっては誤った判断に至る危険のある値でもある。

長期的なデータは予測には不適切な場合がありうる。比較的に短期のデータを使って、統計学的にデータが「信頼できる」という結果が出たならば(K'sのソフトではｐ値が5%以下という検定結果などが出る)、長期的データは不要と思われる。統計学的検定を使って短期のデータを「科学的」に分析すれば、長期のデータは不要で、短期でもより信頼性・予測性の高い結果が出る。

したがって、最先端の統計学的手法を使用しているK'sのソフト(「データ」「さや取り一発」「クイックベータ」など）では、場帳から手入力できる程度のデータ数でも、じゅうぶんに信頼できる結果が得られるのである。また、短期のデータから統計学的に信頼できない結果（ｐ値が5%以上）が出たならば、このような予測結果に依拠する投資行動はリスクが高いというわけである。

統計学的手法を相場の分析に取り入れることで、「投資についてのポリシー」が生まれるのである。