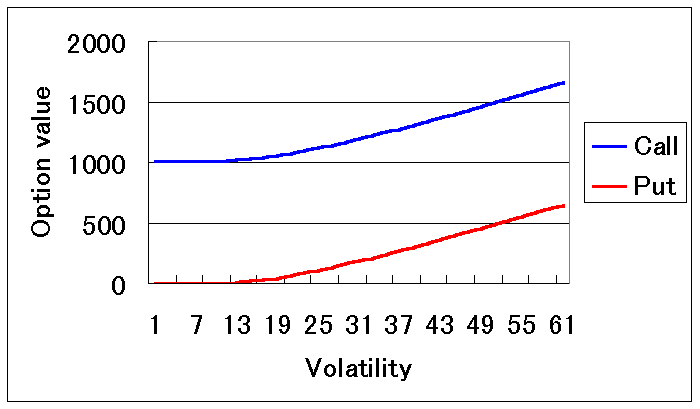
この図は、日経平均オプションの理論価格をブラック・ショールズ式(1997年度ノーベル経済学賞受賞）によって計算してグラフ表示したものです。日経平均が16,000円のとき、行使価格が15,000円、短期金利が0.7％、残存日数が30日というブラック・ショールズ式への入力条件で、シミュレーションしました。ボラティリティーを動かすと、コールとプットがどのように変化するかを表しています。横軸がボラティリティーで縦軸がオプションの理論価格です。

　グラフを見るとわかりますが、ボラティリティーが約13％以下になると、オプションの価格はほとんど変化しません。このようなボラティリティーの値は、入力条件を変えると、もちろん変わります。しかし、このようなボラティリティーの値が存在するため、Spaceなどのソフトを使ってインプライド・ボラティリティーを計算するとき,うまく計算ができなくなることがあります。そのような条件下では、インプライド・ボラティリティーを求めることはできないのです。この例ですと、約13％以下のボラティリティーでしたら、オプションの理論価格はすべて同じなのです。言い換えると、市場価格から一意的にボラティリティーが決まらない、というわけです。デルタが0,1,または-1になったときが、要注意です。これはオプションがかなりインザマネーまたはアウトオブザマネーのときです。

　膨大な過去の取引データに基づく実証研究の結果ですが、ブラック・ショールズ式はオプションがインザマネーまたはアウトオブザマネーのとき、ミスプライシング(誤った値付け)が起こることが知られています。ですから、ブラック・ショールズ式は万能ではなく、アットザマネー近辺の取引で、できるだけ短期の取引においてその力を発揮するものと思われます。

Home