■　株価

以下のようにサイコロの目に対応する株価を使って、標準偏差について説明する。

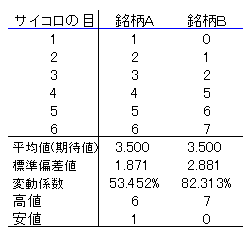
銘柄Ａの株価はサイコロの目そのものである。

銘柄Ｂの株価は、サイコロの目が1,2,3なら、目から1を引いた値が価格である。そして、サイコロの目が4,5,6なら、目に1を足した値が価格である。

■　範囲と変動係数

したがって、銘柄Ａは高くても6円で、安くても1円である。銘柄Ｂは、高くても7円で、安くても0円である。

ということは、銘柄Ｂの方がＡに比べ、価格に幅があることになる。銘柄Ａの範囲(レンジ;range）は

で、銘柄Ｂの範囲（レンジ）は

である。

範囲とは、最大値から最小値を引いた値である。統計学において、範囲は「散らばりの尺度」のひとつである。

このように、高値と安値から価格の範囲（レンジ）を計算すれば、どちらの銘柄が価格に「散らばり」があるかがわかる。

変動係数を見ても、銘柄Ｂの方が価格の「ばらつき」が大きいことがわかる。

ここで、注意すべきことは、銘柄ＡとＢの平均価格が同じことである。株価の平均価格だけでは、「価格のばらつき」について知ることはできない。これは重要ポイントである。

■　期待収益率

証券などの価格の平均は期待される収益に関係する。

期待収益率(expected return)は

と定義される。

したがって、例えば、銘柄Ａの購入価格が3円なら、この期待収益率は

である。

平均価格は、確率論的にいうと、期待値である。1から6までの目が出る確率は、それぞれ1/6である。したがって、各銘柄に投資して得られる期待値(期待価格）は、

と、目が出る確率に価格を掛けて足した値である。これは、結局、それぞれの目が出る確率が等しいので、目に対応する価格の平均値と同じ値になる。

が、仮に、それぞれの目が出る確率が等しくないならば、目に対応する価格の平均値を期待価格とすることはできない。

ここの点に注目していただきたい。仮に「サイコロの目に対応する価格」という「モデル」によって株価が決まると想定しても、それぞれの目の出方が「同様に確からしい」という仮定の下では、上記のごとく期待価格を求めることはできる。しかし、それぞれの目の出方が「同様に確からしくない」という仮定の下では、もはや期待価格を計算することはできなくなる。それぞれの目が出る確率が不明だからである。

■　標準偏差はリスクの指標

投資の世界において、リスクは価格変動であるから、リスクとは「価格のばらつき」である。

銘柄ＡとＢの期待収益率は同じであるが、銘柄Ｂの方が「価格のばらつき」が大きいため、リスクが高い。したがって、銘柄ＡかＢのどちらかを選択するとき、銘柄Ａの方がよいことがわかる。

範囲や変動係数の他に、「価格のばらつき」を示す尺度として、標準偏差(standard deviation)がある。標準偏差でみると、銘柄Ｂの方がＡに比べ、

と、1.54倍のリスクがあるにもかかわらず、期待収益率は同じことになる。

統計学では、標準偏差を二乗した値を分散(variance)という。投資理論では、リスクを標準偏差または分散によって定義することが一般的である。

標準偏差の計算方法については、ここを参照してください。

また、計算方法を知らなくても、以下の2点を覚えておけば、実務的にはじゅうぶん。

1. 価格の標準偏差が大きいほど、価格の「ばらつき」も大きいため、投資リスクが高い。
2. データの約2/3が

   平均　+　標準偏差

   と

   平均　-　標準偏差

   との間に入る。

問題は、いかにしてリスクを低くし、期待収益率を高くするかである。これこそ、近代ポートフォリオ理論(MPT: modern portfolio theory)の基本コンセプトである。

また、価格変動のリスクを価格の標準偏差として定義すると、不都合なことが生じる場合がある。この点については、後の講義で説明する。今の段階では、価格の標準偏差をリスク指標のひとつとして考えておいていただきたい。