![]()
プレミアムの下限値について
ここでは、無配当の株式オプションを基本に、オプション・プレミアムの下限値(floor)について解説する。下限値は本質的価値または本源的価値(intrinsic value)である。
オプションのプレミアムは時間的価値(time value)と本質的価値に分けて考えることができる。本質的価値は権利行使によって確実に得られる利益部分である。満期日においては、プレミアムには本質的価値しかない。時間的価値がゼロだからである。
ヨーロピアン形式のオプションには下限値は1つしかなく、下限値をソフト・フロアー(soft floor)と呼ぶ。が、コールの場合、アメリカン形式には下限値が2つあり、ひとつをソフト・フロアー、もうひとつをハード・フロアー(hard floor)と呼ぶ。
コール・オプションの場合、ハード・フロアはソフト・フロアの下にある。
このような下限値(フロア)は、無配当の株式オプションに適用可能な概念である。が、配当利回りの小さい(1%以下)の株価指数(例えば、日経平均)オプションなどにも適用できる。
Sを原資産価格、Kを行使価格とする。tを時間、rを無リスクの金利(市場短期金利)とする。
ハード・フロアは
である。
ソフト・フロアは
である。
K/(1+r)tは行使価格の現在価値である。maxとは「カッコの中で最大(maximum)の値を取れ」という意味である。
コールの下限値を図で示すと、以下のようになる。
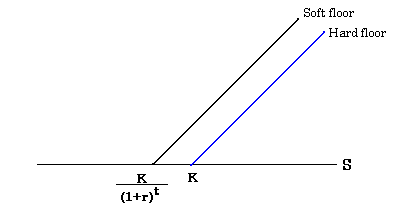
オプションの満期では、t=0であるから、ソフトとハードのフロア(下限値)は同じになる。
Traderで示している直線の損益図はハード・フロアのみである。曲線はブラックショールズによるプレミアムの曲線で、満期が近づくとハード・フロアに近づく。
tの計算であるが、t=1を一年と定義する。したがって、一年が365日ならば、残存日数が90日の場合、t=90/365=0.247である。
例えば、短期金利が1%、残存日数が90日の株券オプション(無配当)で、行使価格が170の現在価値は
である。
このときの株価が180なら、コールのソフト・フロアは
である。
株券オプションはヨーロピアン形式なので、コールの下限値は10.42ということになる。もし、これより市場でのプレミアムが安ければ、コールは割安と判断できる。裁定によって本来の価格に戻るため、割安のコールを買うことでプレミアム益が狙える。
また、10.42よりコールのプレミアムが安くなってはならない根拠であるが、アービトラージ理論によって説明できる。
株価が180のとき、2通りのポートフォリオが考えられる。
いずれの場合も、投資元本は180円である。しかし、1と2では、異なる点がある。2では損失が限定されることである。
ポートフォリオ2の場合、無リスクの短期金利で169.58円を90日間運用すると、オプションの満期には170円の元本が戻る。もし、株価が行使価格の170円以下ならば、コールを行使しなければよい。170円より高ければ、コールを行使して無リスクの短期金利で運用された170円で株を買えばよい。したがって、株が上がろうと下がろうと、170円が損失の下限値である。
ところが、コールがソフト・フロアーの10.42円より割安になると、180円よりも少ない投資元本で、上記2のポートフォリオがつくれる。このような状況なら、投資家は180円で株を買うよりもコールを買うであろう。したがって、コールの価格はソフト・フロアの10.42円以上に押し上げられる。
プットの場合、ハードとソフトの下限値は逆になる。
ハード・フロアは
である。
ソフト・フロアは
である。
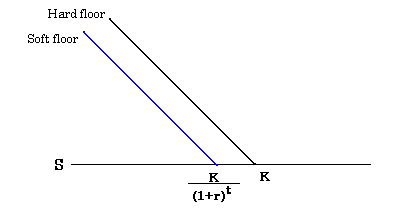
Traderで示している直線の損益図はハード・フロアのみである。曲線はブラックショールズ式によるプレミアムの曲線である。プットの場合、ソフトはハードの下に位置するため、ブラックショールズ式による理論価格はハード・フロアを割り込む。
アメリカン形式のプットにおいて、下限値はハード・フロアのみである。
では、ハードとソフトのフロアは、いかに実際の取引に応用できるか。
例えば、日経平均オプションのプレミアムを見ると、ソフト・フロアよりも割安の市場価格が頻繁に観測される。このようなプレミアムには、インプライド・ボラティリティー(IV)は無意味である。
IVとは無関係に、このようなプレミアムは割安である。売り手になる場合は不利で、買い手にとっては有利と考えられる。バーゲン価格のようなものであるから、購入し本来の価格に戻ったときに転売すればよい。が、残存日数が少ないときは、要注意である。本来の市場価格に戻る前に、オプションという権利が消滅する可能性が大きい。

Spaceを使えば、ソフト・フロアを簡単に計算できる。最小値というのが、プレミアムのソフト・フロアである。このソフトウェアでは割引ファクターに(1 + r)tは使用せず、ertという連続複利計算法を用いている。この図で示した例の場合、10.4187がコールの本質的価値で、
16.4061 - 10.4187 = 5.9874 がコールの時間的価値である。
このようにソフトウェアを使って理論価格を計算し、割安か割高かを判断すれば、リスクを最小にリターンを追及することができる。
以上のように、短期金利が高いと、ハードとソフトのずれは大きくなる。アメリカン・オプションの場合、ブラックショールズでは近似できなくなる。ブラックショールズ式は、ヨーロピアン形式の無配当の株式オプションに適用されるモデルである。ヨーロピアン形式のオプションにおいて、フロアはソフト・フロアのみである。
配当や原資産に利回りなどがあると、配当落ちなどによって原資産の価値はその分下る。例えば、コールの場合、プレミアムは株価がある価格以上になると本質的価値を下回り、ソフト・フロアを割り込む。つまり、時間的価値は負の値をとることになる。時間的価値がマイナスのオプションを保有するのは不利。アメリカン形式では、配当落ちや、債券オプションでは利払いが生じると、必ず権利行使される。通常は配当や利払いの直前に権利行使されることが多い。ここで、配当や利払いなどの原資産から発生するキャッシュフローは連続的に支払われるものと仮定する。
日経平均の場合、配当率が小さいので(通常は1%以下)、無配当のブラックショールズ式で評価してよいと思われる。が、アメリカの株価指数取引では、配当率を考慮し「利回りのあるブラックショールズ式」で評価すべきである。これはブラックショールズ式をノーベル経済学賞を受賞したロバート・マートン(Robert Merton)が改良したもので、「マートンのモデル」などとも呼ばれる。ちなみに、マートンの父親はコロンビア大学教授で、アメリカを代表する社会学者(sociologist)である。
配当などがなく、満期までの時間的価値がある場合、期限前行使には大きなメリットはない。特にコールの場合、権利行使するよりもコールを転売してから、原資産を買った方が有利である。プットの場合は、ヘッジが目的であることが多いので、期限前行使される確率は高い。少なくとも、コールに関しては、アメリカン形式のオプションであってもブラックショールズ式で評価可能と考えられる。ただし、これは原資産に配当や利払いがない場合である。
Traderを使って、プレミアムが金利や原資産から生じるキャッシュフローなどによって、どのように変化するかを考えてみよう。
このソフトでは、以下のオプション評価モデルが利用できる。
適当にいろいろな値を入れてみて、ハード・フロアを下回る場合などについて、考えてみよう。