それでは、 自己発生的な街にどのような原理が働いているのかを考えてみようと思います。 仮説として、 一つ考えているのは、 早い者勝ちのルールです。 これは、 生物の発生の原理として言われたりしています。 例えば、 これは蝶の燐粉ですが、 こういう不整形でランダムなものがどのようにできるのかを見てみると、 それぞれの細胞の成長速度にばらつきがあって、 そのばらつきがあるものに対して早い者勝ちのルールを入れると、 こういった不整形なパターンが作り出されるということをコンピューターでシミュレートしたものです。

自己生成的な街がなぜ不整形になりがちかということを考えてみると、 一つはこういった早い者勝ちのルールがあるのではないかと思います。 人間社会の場合には強いもの勝ちということもありますが、 基本的には早い者勝ちということが考えられます。

その結果、 初期的な条件に対して非常に敏感になってきます。 初期的にどういうふうな形になったのか、 あるいは、 初期にどういうものがあったのかということが、 あとあとの街の構造を決定づけていくということがいえるかと思います。

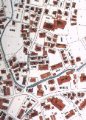
右側のスライドは、 先ほどの東京都の稲城市の図です。 所々に白く残っているところがナシ畑で、 そういうところが市街化していきますから、 あちこちでばらばらな方向を向いた建物が建てられつつあります。 こういうところでは、 ナシ畑が街の骨格を作っていったり、 あるいは水路があったりすると、 街の構造を決めていったりします。 このように、 早い者勝ちというか、 先にあったものが次の構造を規定していくというような傾向が見られると言えます。

もう一つ重要な点は、 こういった自己生成的で不整形な街は、 街自体をいくつかのモジュールで区切って、 それがいくつ集まったらどんな単位になって、 その時にはどれぐらいの幅員の道が発生して、 ということでは推し量れない、 非モジュール的な空間であるということがいえると思います。

右は、 サントリーニのイア（Ia）という街ですが、 どこで単位というものが設定できるのかは非常に難しいと思います。 サントリーニの街は、 もともと港町で、 貿易中継港だった街です。 船主あるいは船長が尾根の一番上に大きな家を構えていて、 クルーが自分たちの船が見える斜面に居を構えたというのが基本的な形です。 空間的には、 これをあるモジュールで分解することはできません。 あるモジュールをいくつか集めると全体ができるということではありません。

左はマレーシアのコタキナバル（Kota Kinabalu）という水上集落です。 これも、 モジュール単位ではなく、 必要に応じてだんだん成長していった町です。

こういう自己生成的な街は、 モジュールに分解できないし、 モジュールを積み重ねても全体像が作り出せないということです。 それぞれの建物とその間の道が密接な相互関係にあって、 全体として一つの有機体として形成されているとということだろうと思います。

これは、 ギリシャのロードスです。

左は紀元前5世紀頃の、 いわゆるギリシャの植民地都市であった頃の復元図です。

右は現在の姿です。 左側のスライドに見られた整然たる街割がものの見事に現在まで残っていません。 人類は2,500年かけて、 左側のスライドようなものを右側のスライドのように作り替えていったということが、 今日の私の結論の一つであります。